通达信皮氏积矩副图(原理、说明)
原理:
相关系数定义与说明:皮(尔逊)氏积矩相关系数
相关系数又称线性相关系数.它是衡量变量之间线性相关程度的指标。相关系数的取值范围为[-1,1]。
相关系数值越大,误差越小,变量之间的线性相关程度越高;
相关系数值越接近0,误差越大,变量之间的线性相关程度越低。说明两个现象之间相关关系密切程度的统计分析指标。
相关系数值的范围在-1和+1之间。相关系数>0为正相关,相关系数<0为负相关。相关系数=0表示不相关;
相关系数的绝对值越大,相关程度越高。
两个现象之间的相关程度,一般划分为四级:
如两者呈正相关,相关系数呈正值,相关系数=1时为完全正相关;
如两者呈负相关则相关系数呈负值,而相关系数=-1时为完全负相关。
完全正相关或负相关时,所有点都在直线回归线上;
点子的分布在直线回归线上下越离散,相关系数的绝对值越小。
当例数相等时,相关系数的绝对值越接近1,相关越密切;越接近于0,相关越不密切。
当相关系数=0时,说明X和Y两个变量之间无直线关系。
通常相关系数大于0.8时,认为两个变量有很强的线性相关性。
相关系数的性质:
(1)相关系数可正可负;
(2)相关系数的区间是[-1,1];
(3)具有对称性;
(4)相关系数与原点和尺度无关;
(5)如果X与Y统计上独立,则它们之间的相关系数为零;但是相关系数=0不等于说两个变量是独立的。即零相关并不一定意味着独立性;
(6)相关系数是线性关联或线性相依的一个度量,它不能用于描述非线性关系;
(7)虽然相关系数是两个变量之间的线性关联的一个度量,却不一定有因果关系的含义;
使用方法仔细看就可以一目了然了。红买绿卖一看就会。这里也就不多说了。如有高手加以延伸则更上一层楼。
日线示意图:
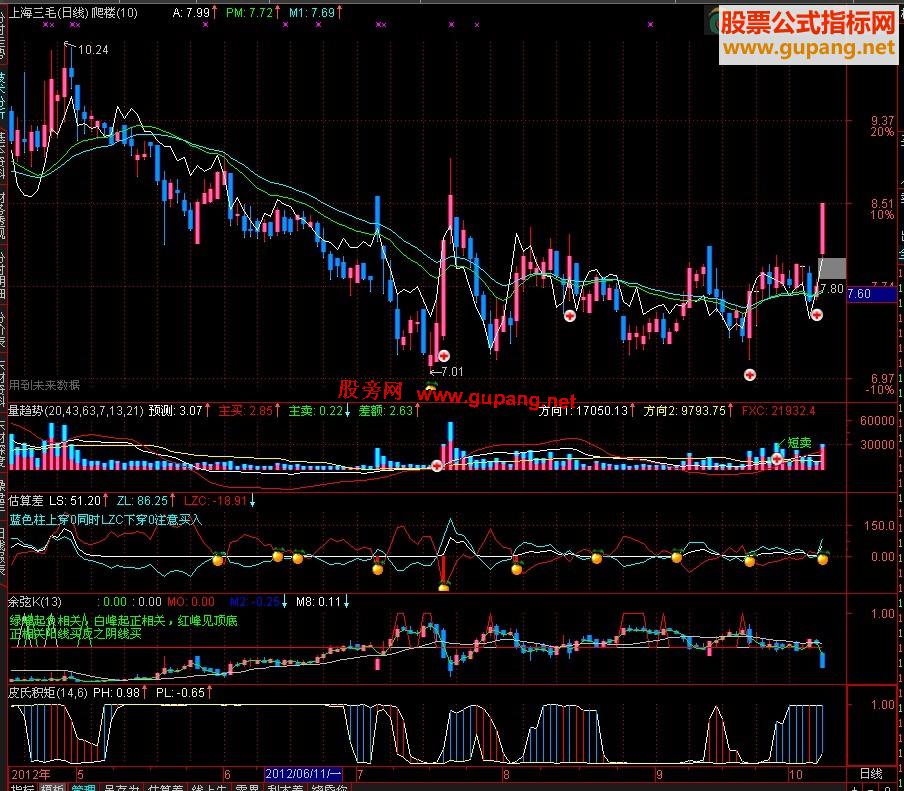
代码:
PH:RELATE(COS(H),SIN(H),5);
PO:=RELATE(COS(O),SIN(O),5);
PC:=RELATE(COS(C),SIN(C),5);
PL:RELATE(COS(L),SIN(L),5);
STICKLINE(PC>=PO,PL,PH,0.00001,0),COLORFF9900;
STICKLINE(PC<PO,PL,PH,0.00001,0),COLORRED;